鈦酸鋰電池憑借著出色的功率性能和優異的循環壽命，在動力鋰離子電池領域得到了一席之地，在一些對快充和低溫性能要求較高的領域得到了應用。等效電路模型是模擬鋰離子在放電過程中電壓和溫度變化的有效工具，但是傳統的等效電路模型在較寬的電流和溫度范圍內，擬合效果并不理想。

 

       近日，北京交通大學的AnciChen（第一作者）和Weige Zhang（通訊作者）、Caiping Zhang（通訊作者）等人通過將修正Bulter-Volmer公式和Nernst公式應用在等效電路模型之中，從而使得等效電路模型適應了不同溫度和電流范圍，從而顯著提升了仿真精度。

 

       鈦酸鋰電池在使用過程中通常會面臨大電流的使用工況，會導致電池溫度在較大的范圍內波動，因此對電池更為準確的模擬需要充分考慮溫度和電流的相互影響。通常鋰離子電池的模型可以分為三大類:1）電化學模型；2）數學模型；3）等效電路模型。電化學模型能夠根據電池內部的反應機理對電池的充放電行為進行模擬，但是這一模型的復雜程度較高。對于數學模型而言，通常是借助經驗公式或數學方法獲得電池的模型，但是這種方法中的參數缺少準確的物理含義，因此模擬的準確度較低。等效電路模型則是采用各種元器件模擬電池電流和電壓，從而實現在較少的參數的前提下，獲得較高的擬合準確度。

 

       為了提升等效電路對溫度和電流的適應性，常見的辦法時建立一個隨溫度和電流變化的參數查詢表，但是這種方法缺少理論依據，因此參數表的準確性對模型準確性會產生顯著的影響。為了提升模型的準確性，人們嘗試將等效電路的參數在理論的基礎上建立與溫度和電流的關系，例如Zhu等人就通過阿倫尼烏斯公司對Butler-Volmer公式進行修正，從而建立了電荷交換阻抗與溫度和電流之間的關系，但是這種方法的誤差較大。

 

       在該項研究中作者采用了傳統的等效電路模型的基礎上，考慮了溫度和電流對于模型參數的影響，作者對BV等式進行了修正和簡化，然后整合到了整個模型之中，同時為了反映溫度對于開路電壓的影響，作者在等效電路模型中引入了Nernst公式。采用多項式修正的方法對溫度對電池歐姆阻抗的影響進行了分析。

 

       電池的等效電路模型通常可以根據兩種機理構建，一種時基于交流阻抗構建的等效電路，能夠模擬電池對頻率的響應特征，但是對直流的響應的模擬并不好，同時計算的復雜程度還比較高。另外一種時基于Thevenin的等效電路模型（如下圖所示），其中包含一個電壓源，R0則主要反應電極、電解液和隔膜的歐姆阻抗，而RC并聯電路主要用來反應電極的電池極化和動力學特性。

 

       在這里作者采用了1維的等效電路，這主要是因為1維模型的就能夠對電池的行為進行較為準確的模擬，其次是這種模型能夠更為準確的對高功率電池進行模擬。

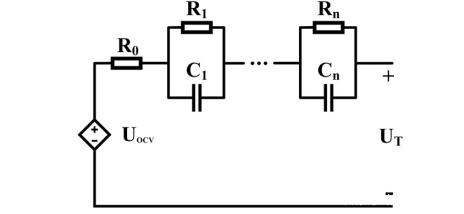
       為了能夠分析SoC、溫度、電流和電流方向對于電路參數的影響，作者引入了能斯特方程等原理。

 

       Ⅰ能斯特方程

 

       電池的電壓主要反應電池儲存的能量，受到溫度的影響，根據能斯特方程電池的開路電壓與溫度的關系如下式所示，其中R為氣體常數，T為絕對溫度，z電化學反應交換的電子數，F為法拉第常數，Q為反應物的比例（在這里作者認為電池內部的反應物的濃度變化可以忽略，因此Q為定值），值得注意的是下式中的參數都與溫度無關，但是與電池的SoC狀態密切相關。

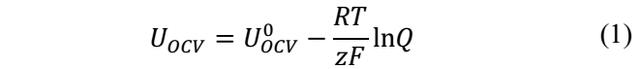
      Ⅱ BV公式的再修正

 

       BV公式是最重要的電化學動力學公式，主要描述了電流密度與穩態過電勢之間的關系（如下式所示），其中j為電流密度，j0為交換電流密度，α為對稱系數，ηmax為穩態電化學過電勢。

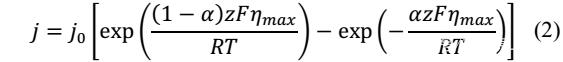
       上述公式僅能夠在固定的溫度下使用，因為交換電流密度j0與溫度之間存在密切的關系，根據交換電流密度的定義，作者給出了如下所示的交換電流密度的定義公式，其中Aa為常數項，[R]表征反應物的濃度，φe表征電極的電勢，Ea0則表征反應的活化能，

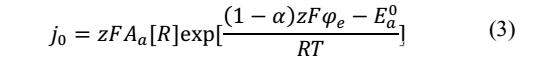
       根據Nernst公式，φe可以采用下式4進行表征，Ea0則可以通過下式5表征為溫度的函數，m為一個無關溫度的常數。

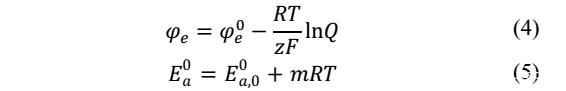
       開路電壓可以用下式進行表征

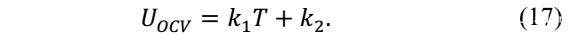
   電池的電流密度可以根據電池的電流和有效面積求得

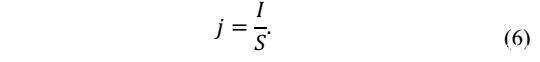
       根據上面的推斷，BV方程則可以轉化為如下式7所示的形式，研究表明對稱系數α在實際中基本上都在0.5附近，很少變化，對公式7進行求解，結果如下式8所示的形式。下式8中所有的參數都與溫度和電流無關，僅與電池的SoC有關，因此我們可以根據公式8對電池對電池在不同的電流和溫度下的電壓特性進行模擬。

       由于在上式8中所有的參數都僅與SoC狀態有關，因此該模型可以進一步簡化為下式

 

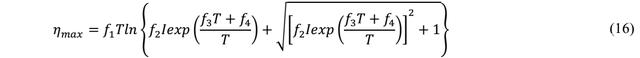
       電池歐姆阻抗基本不受電池電流的影響，但是卻受到溫度的顯著影響，但是研究表明歐姆阻抗R0受溫度影響的規律并不符合阿倫尼烏斯公式，因此作者在這里采用了一個多項式描述歐姆阻抗受到溫度的影響（如下式所示），其中P1、P2和P3分別多項式的系數

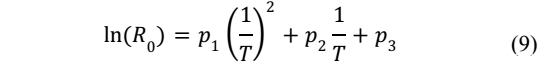
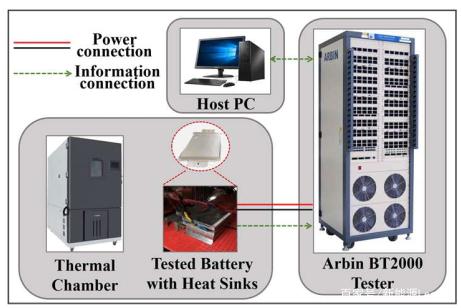
       測試系統如下所示，包含測試設備、恒溫箱和電池，電池的基本信息如下表所示

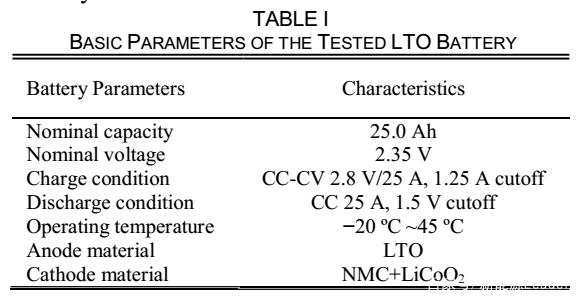
       首先作者測試了電池的容量，具體步驟為采用CC-CV制度對電池進行充電，然后以1C倍率下進行放電，以測量電池的容量，重復該過程3次，以得到平均電池容量。然后作者分別在5℃、15℃、25℃和45℃測試了電池在10%-90%SoC范圍內，電池的開路電壓和歐姆阻抗。然后作者采用FUDS測試（如下圖所示）驗證了模型的準確性。

       該模型的整體運行流程如下圖所示，其中修正后的BV公式能夠為模型提供不問溫度和電流下的極化信息，Nernst公式則可以用來描述不同溫度下的開路電壓特征。

 

       實驗中作者將電池的工作定義為電池在給定的SoC和溫度T下首先以電流I（正為充電，負為放電）工作時間t，然后靜置t1時間，因此電池的SoC狀態可以通過下式積分求得，其中Cap為25℃條件下電池在1C倍率下的放電容量。

 

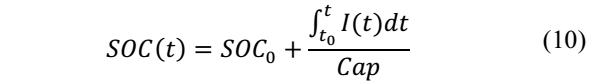
       因此模型中與SoC相關的參數可以表述為下式

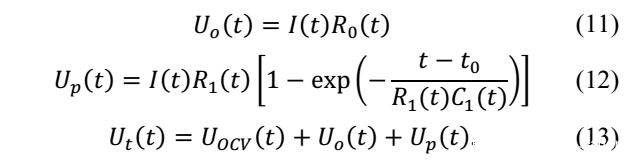
       在靜置條件下電池的開路電壓可以用下式進行描述，在模型中作者對于電容C的數值沒有進行專門的設計，這主要是因為電容C的數值對于模型準確性的影響較小，因此作者將RC并聯電路的時間常數固定在15s。模型中與SoC相關的參數1, 2, 3, 1, 2, 3, 4, 1 2則是根據最小二乘法擬合利用線性插值的方式獲得。同時由于作者假設忽略濃差極化的影響，但是在充放電末期時濃差極化較為顯著，因此不能不忽略，因此該模型僅適合模擬電池在10%-90%SoC范圍內電池的行為。

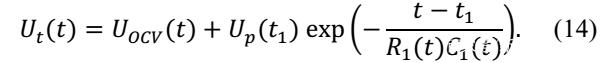
       等效電路模型的首先要做的工作就是確定電池的開路電壓，下圖中展示了快速測量鈦酸鋰電池開路電壓的方法，電池以1C倍率進行充放電，每5%SoC電池靜置5min，然后根據充電和放電電壓作者得到了下圖中綠線所示的開路電壓曲線。

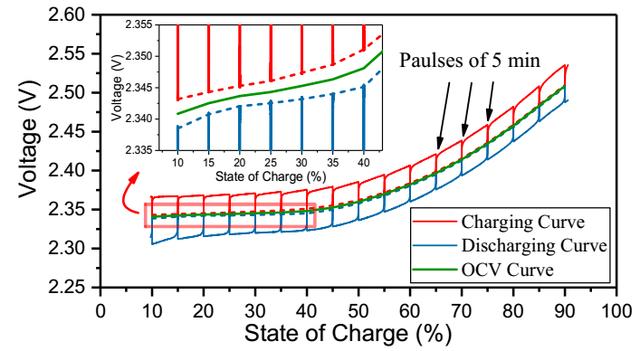
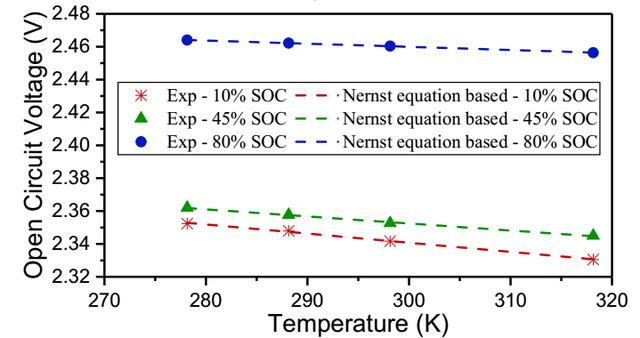
       接下來作者分別測試了在5℃、15℃、25℃和45℃下的開路電壓，如下圖所示

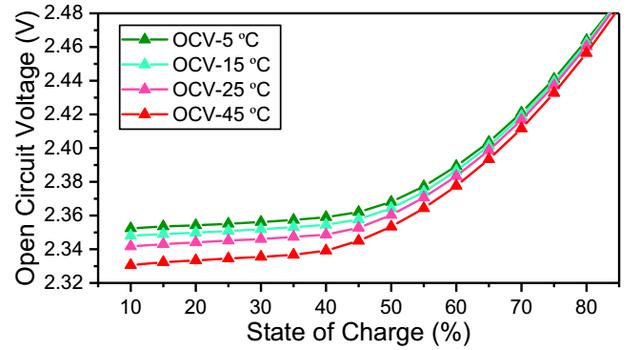
       在下圖中作者分別根據Nernst方程計算了電池在10%、45%和80%SoC狀態下電池的開路電壓與溫度之間的關系，可以看到計算結果與實際結果符合的非常好。

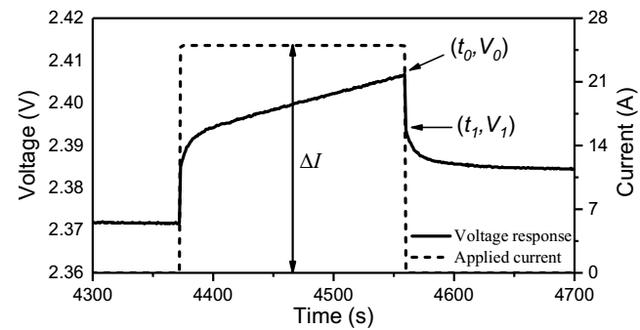
       下圖為電池在放電過程中靜置期間的電壓變化，我們可以根據電流變化瞬間引起的壓降計算電池的歐姆阻抗（如下式所示），這里兩次取樣時間的間隔設定為1s，這主要是因為電池的極化通常需要數十秒，甚至是數百秒的時間達到平衡，因此在1s的時間內電池的極化不會發生顯著的變化，因此此時的電壓變化主要來自于電池的歐姆阻抗。

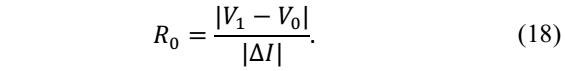
       下圖為作者根據阿倫尼烏斯公式繪制的在特定的SoC狀態下電池的歐姆阻抗與溫度之間的關系，從圖中能夠看到兩者呈現非線性的關系，這表明歐姆阻抗與溫度之間并不遵循阿倫尼烏斯公式，因此作者在這里采用一個多項式對電池的歐姆阻抗與溫度之間的關系進行了描述，從同種能夠看到擬合結果與實測結果之間符合的非常好。

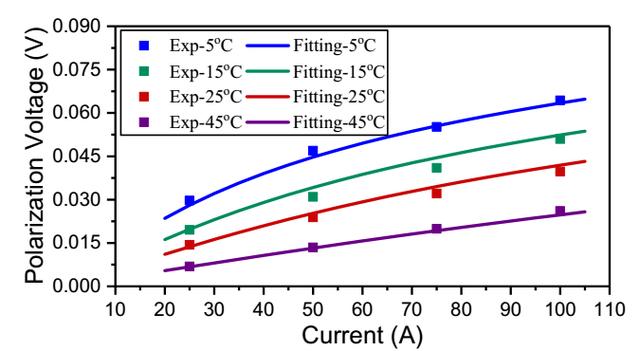
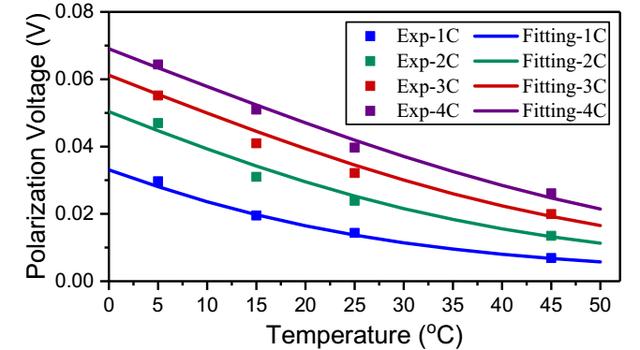
       在上面我們已經獲得了電池的開路電壓和歐姆阻抗R0，因此我們可以根據上式16來計算電池的穩態極化電壓，在這里作者采用了恒流充電過程中的數據，以確保電池的極化達到穩態。下圖分別為電池在不同的溫度下以不同的電流進行充放電的極化電壓數據，從圖中能夠看到溫度和電流對于電池開路電壓的影響是呈現非線性的關系，作者在這里采用修正的BV公式獲得了擬合結果，從圖中能夠看到仿真結果與實測結果最大誤差約為2.2mV。

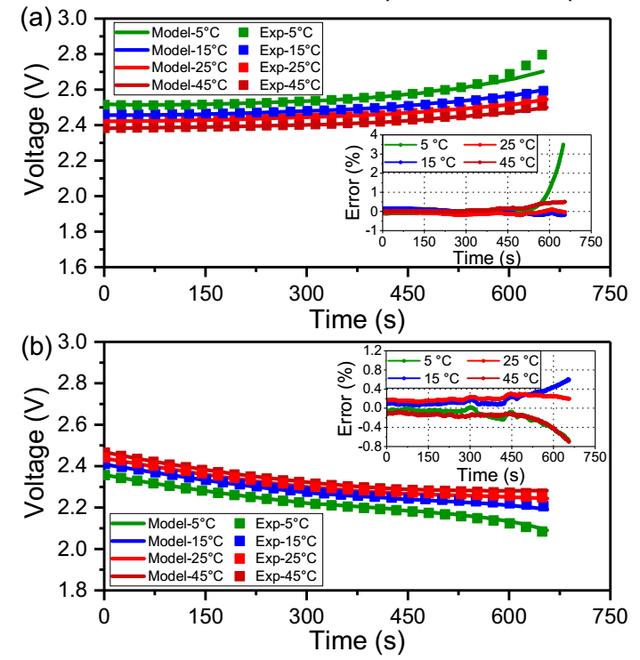
       為了進一步驗證模型的有效性，作者采用在不同溫度下4C恒流充放電的形式對電池進行了測試，從下圖a的充電工況模擬結果可以看到，在前516s中擬合誤差在0.2%以內，在516s后誤差也控制在-0.2%至0.5%之間，僅在5℃下誤差增長較快達到3.5%，這主要是受到低溫下電池較低的傳質速率的影響，因此濃差極化的影響不能再被忽略，導致誤差升高。

 

       下圖b則展示了在不同溫度下的4C放電數據，從圖中能夠看到在整個放電過程中，不同溫度下模型擬合的結果都非常好，誤差都在0.8%以內。

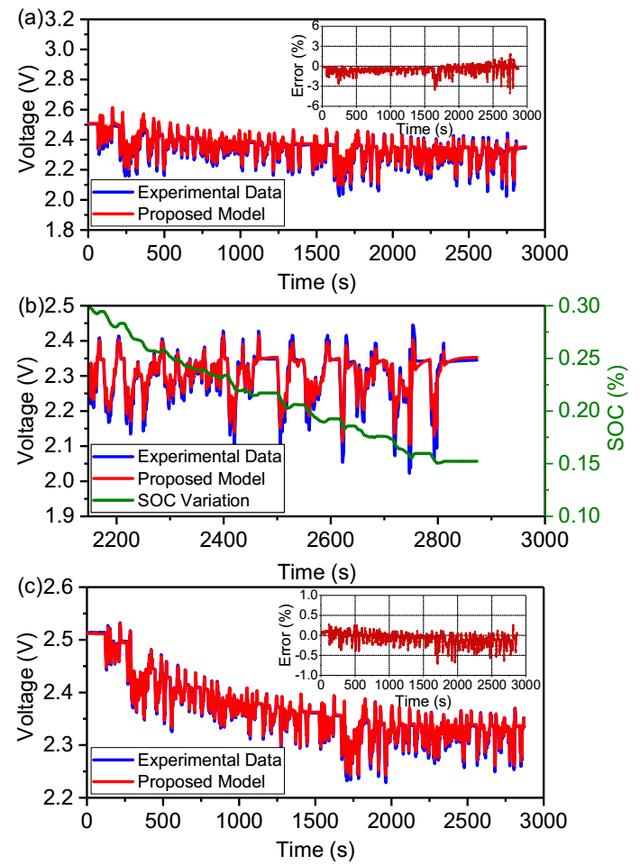
       接下來作者采用更為復雜的FUDS制度對模型的準確性進行了檢驗，電池的最大電流可以達到8C左右，從下圖a中可以看到即便是在如此復雜的使用工況中，模型對于電壓預測的最大誤差也僅為-4%與1.7%之間，從下圖c中可以看到在35℃的條件下模型能夠獲得更好的預測精度，誤差僅為-0.7%至0.3%之間，這主要是因為高溫下良好的傳質速率，消除了濃差極化造成的影響。

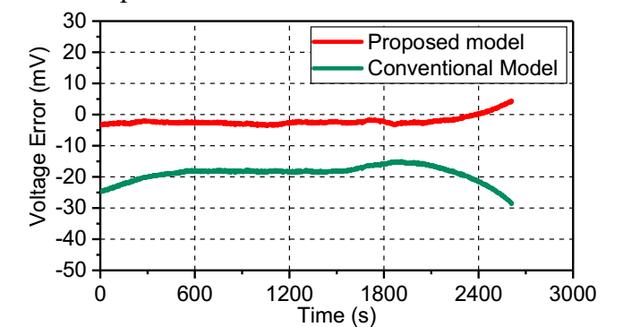
       下圖中作者對比該修正后等效電路模型與傳統的等效電路的模擬效果，當電池在1C倍率放電和5℃的條件下，傳統的等效電路模型的誤差要明顯的高于修正后的等效電路模型，傳統的等效電路模型的誤差為-14.86mV至-28.68mV之間，而修正后的模型的電壓誤差則僅為-3.68mV至4.45mV之間。

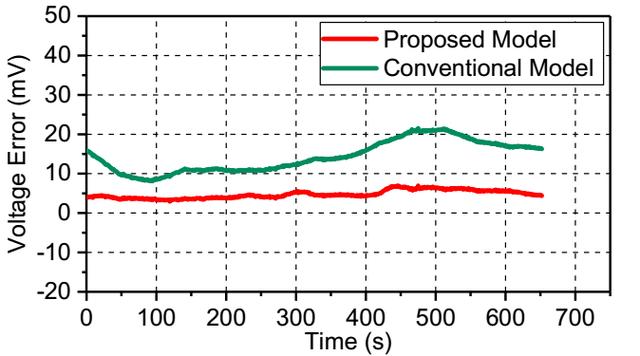
       下圖作者對比了常溫下，4C倍率放電時兩種等效電路模型的誤差范圍，從圖中能夠看到傳統的等效電路模型的電壓誤差在8.09mV至21.55mV之間，而修正后的等效電路模型小于6.94mV。

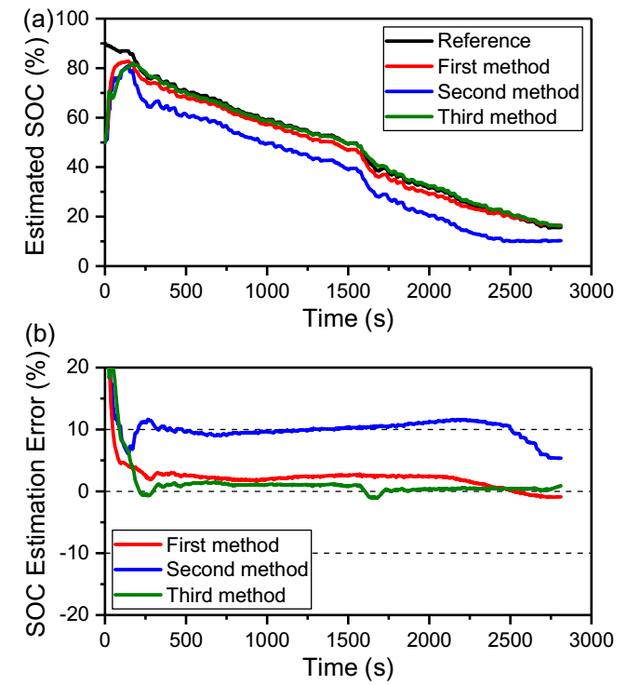
       下圖為作者在5℃下采用FUDS循環對模型預測電池SoC狀態預測的結果，其中第一種方法時基于修正后的等效電路模型，以及卡爾曼濾波函數，第二種方法時基于傳統的等效電路模型和卡爾曼濾波函數，第三種方法是基于一維等效電路模型和雙卡爾曼濾波函數。從下圖的預測結果可以看到第一種和第三種方法都取得了較高的預測精度，其中第一種方法的誤差為-0.99%至3.02%，第三種方法的預測誤差在-1.13%至1.51%，而第二種放大的誤差則達到了5.34%至11.6%之間，三種方法的平均誤差分別為1.82%、9.89%和0.68%，可以看到修正的等效電路模型對于SoC狀態的預測取得了較高的精度。

       Anci Chen通過利用能斯特方程和阿倫尼烏斯方程等工具，將溫度和電流對于電路參數的影響引入了一維等效電路模型，從而大大提升了模型預測的準確度。